| (4.2) |
| (4.2) |
 |
(4.3) |
L'utilisation
de déterminants séparés pour des rotations de différence, aboutit
à une fonction d'essai qui n'est pas antisymétrique en ce qui concerne l'échange
d'électrons de rotation opposés, mais donne les valeurs à peu près correctes pour
des opérateurs indépendants de rotation. [23]
le facteur Jastrow![]() , dans le cas le plus général, est une fonction de l'électron
et des positions d'atome. Plus de choses sur les fonctions Jastrow sont dans la section suivante.
, dans le cas le plus général, est une fonction de l'électron
et des positions d'atome. Plus de choses sur les fonctions Jastrow sont dans la section suivante.
La partie determinante du wavefunction est d'habitude obtenue
d'une méthode cohérente comme LDA-DFT ou
HF. [37,38] Pour la plupart des
calculs dans cette thèse un produit simple d'en haut et les déterminants d'en-bas rotationne
d'orbitalements, elle est utilisé pour former le wavefunctions. En principe,
l'interaction de configuration ou des calculs de multi-configuration peuvent être
utilisés pour fournir des déterminants multiples, y compris les
coefficients![]() ,4.3 Mais beaucoup de d'applications de QMC ont
démontré qu'une haute exactitude qui peut d'habitude être obtenue en utilisant seulement
un déterminant simple.
,4.3 Mais beaucoup de d'applications de QMC ont
démontré qu'une haute exactitude qui peut d'habitude être obtenue en utilisant seulement
un déterminant simple.
L'orbite![]() , est étendu dans
un jeu de base de point de vue quantitative commode. En principe l'orbite pourrait être étendu
dans une
base qui est optimale pour QMC. Le critère clef serait la vitesse d'évaluation
de la valeur et les deuxièmes dérivées de l'orbite
aux points arbitraires dans l'espace. Cependant, peut être que l'on peut obtenir de
l'intérieur un arrangement cohérent la base doit être commode pour résoudre
les équations de particule simple. Par conséquent, des réseaux numériques radiaux,
Gaussian des fonctions [39] et
des vagues de signaux [40] sont typiquement utilisés pour la branche de l'atomique,
moléculaire et certain systèmes.4.4
, est étendu dans
un jeu de base de point de vue quantitative commode. En principe l'orbite pourrait être étendu
dans une
base qui est optimale pour QMC. Le critère clef serait la vitesse d'évaluation
de la valeur et les deuxièmes dérivées de l'orbite
aux points arbitraires dans l'espace. Cependant, peut être que l'on peut obtenir de
l'intérieur un arrangement cohérent la base doit être commode pour résoudre
les équations de particule simple. Par conséquent, des réseaux numériques radiaux,
Gaussian des fonctions [39] et
des vagues de signaux [40] sont typiquement utilisés pour la branche de l'atomique,
moléculaire et certain systèmes.4.4
Une nouvelle façon consiste en ce que l'orbite dans les déterminants doit être des fonctions purement réelles. Dans la supercellule (la condition périodique de frontière) des calculs, c'est réalisé en choisissant les jeux de bloch orbitals tel que les combinaisons linéaires simples de l'orbite rapportent des fonctions réelles.
Le numéro des formes de facteur Jastrow qui ont aimé l'utilisation répétée dans des applications de structure électroniques est limité. Dans cette section, trois formes sont présentées, dont deux est utilisé dans des calculs suivants. Une étude minutieuse de l'efficacité des différentes formes serait difficile de produire en raison du coût informatique impliqué. Alexandre et Coldwell [41] ont passé en revue 118 essai wavefunction des formes pour des atomes, mais n'ont pas considéré d'autre espèce, ou moléculaire et de certains systèmes.
Bien que l'on puisse juger la qualité d'une fonction de Jastrow
les énergies VMC obtenues pour le candidat, les systèmes de compromis doivent inévitablement
être utilisé. L'exactitude d'évaluation de performance des facteurs Jastrow pour le moléculaire et
des systèmes de continuum consiste typiquement en très grands nombres de paramètres. L'augmentation de l'exactitude augmente inévitablement les calculs. Par conséquent, une obtention de wavefunction
![]() de l'énergie de corrélation et 30 paramètres peut être préférable
à une obtention
de l'énergie de corrélation et 30 paramètres peut être préférable
à une obtention ![]() de l'énergie de corrélation avec 200
paramètres. Pour l'utilisation comme une direction DMC wavefunction, plus simple serait préférable en
raison du coût informatique inférieur. Pour des calculs VMC, la préférence dépendrait
de la spécificité d'application pour avoir l'exactitude finale.
de l'énergie de corrélation avec 200
paramètres. Pour l'utilisation comme une direction DMC wavefunction, plus simple serait préférable en
raison du coût informatique inférieur. Pour des calculs VMC, la préférence dépendrait
de la spécificité d'application pour avoir l'exactitude finale.
 |
(4.4) |
| (4.5) |
 |
(4.6) | ||
 |
(4.7) |
Cette forme fonctionnelle a rapporté des exactitudes suffisante pour exécuter des calculs DMC dans plusieurs systèmes, mais n'a pas été systématiquement évaluée pour l'exactitude et la convergence d'énergies VMC.
Bien qu'avec succès utilisé dans plusieurs calculs, la forme fonctionnelle
a deux fonctions indésirables. La fonction de corrélation![]() , est longtemps
étendue impliquant que la somme sur des électrons et des ions n'est pas aisément
la plus rapide i et augmentera donc le coût avec la taille de système. Pour les certaines valeurs
de
, est longtemps
étendue impliquant que la somme sur des électrons et des ions n'est pas aisément
la plus rapide i et augmentera donc le coût avec la taille de système. Pour les certaines valeurs
de![]() , la longue gamme du terme exponentiel exige l'utilisation
d'addition Ewald (la section 4.6.1) dans
des calculs de supercellule. Comme cette somme implique toutes les paires d'électrons, cette
opération deviendrait coûteuse. { 4.6.1}
, la longue gamme du terme exponentiel exige l'utilisation
d'addition Ewald (la section 4.6.1) dans
des calculs de supercellule. Comme cette somme implique toutes les paires d'électrons, cette
opération deviendrait coûteuse. { 4.6.1}
De plus, la fonction n'est pas linéaire dans les paramètres ![]() ,
qui serait désirables d'éviter pour ne pas recalculé la fonction comme
les paramètres sont changés pendant l'optimisation. Cela augmente
le coût informatique de l'optimisation (voir la section 4.7.1). { 4.7.1}
,
qui serait désirables d'éviter pour ne pas recalculé la fonction comme
les paramètres sont changés pendant l'optimisation. Cela augmente
le coût informatique de l'optimisation (voir la section 4.7.1). { 4.7.1}
 |
(4.8) |
La partie dépendante électronique-électronique de la fonction de Jastrow consiste
en une partie cusp- assez satisfaisante et une expansion de puissance qui sont séparée, dont
les deux ont des contraintes pour être courte. Pour la partie cusp- ,
la forme suivante a été choisie :
Les paramètres![]() ,
, ![]() sont différents pour la rotation des paires d'électrons parallèles et anti-parallèles, au modèle. La répulsion
Pauli complémentaire est
expérimentée avec des électrons de rotation parallèles. Ces fonctions donnent
satisfaction l'électron électronique cusp conditionne et est continu dans la valeur de la
première dérivée. La gamme d'expansion
sont différents pour la rotation des paires d'électrons parallèles et anti-parallèles, au modèle. La répulsion
Pauli complémentaire est
expérimentée avec des électrons de rotation parallèles. Ces fonctions donnent
satisfaction l'électron électronique cusp conditionne et est continu dans la valeur de la
première dérivée. La gamme d'expansion![]() , est choisie pour être moins ou
égale au rayon Wigner-Seitz dans des calculs de supercellule évitant
le besoin d'exécuter une somme d'Ewald. Un nouvel avantage
de l'expansion Chebyshev consiste en ce que la différence des termes dans une expansion de
puissance,
les termes portent le poids égal sur leur gamme et exposent
par conséquent la stabilité plus grande pendant l'optimisation.
, est choisie pour être moins ou
égale au rayon Wigner-Seitz dans des calculs de supercellule évitant
le besoin d'exécuter une somme d'Ewald. Un nouvel avantage
de l'expansion Chebyshev consiste en ce que la différence des termes dans une expansion de
puissance,
les termes portent le poids égal sur leur gamme et exposent
par conséquent la stabilité plus grande pendant l'optimisation.
Dans des applications au carbone et de silicium, wavefunctions l'obtention
![]() du fixer-noeud grace à la méthode DMC l'énergie de corrélation à été obtenu.
La haute exactitude de ces wavefunctions indique
que la forme des fonctions de corrélation ne limite pas
les exactitudes obtenues.
du fixer-noeud grace à la méthode DMC l'énergie de corrélation à été obtenu.
La haute exactitude de ces wavefunctions indique
que la forme des fonctions de corrélation ne limite pas
les exactitudes obtenues.
Une expansion de puissance générale, dans ![]() et
et![]() , d'un atome sur
une gamme
, d'un atome sur
une gamme ![]() doit satisfaire des conditions semblables à la fonction de Williamson,
ci-dessus : la fonction doit aller au zéro
doit satisfaire des conditions semblables à la fonction de Williamson,
ci-dessus : la fonction doit aller au zéro ![]() et être continue dans la
valeur et la première dérivée. L'atome a centré l'expansion de puissance dans
la distance d'ion électronique
et être continue dans la
valeur et la première dérivée. L'atome a centré l'expansion de puissance dans
la distance d'ion électronique ![]() et la distance électronique-électronique
et la distance électronique-électronique ![]() contient 5
série indépendante : [48,49]
contient 5
série indépendante : [48,49]
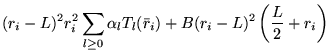 |
(4.13) | ||
 |
|||
 |
|||
 |
|||
 |
| (4.14) |
Le facteur Jastrow complet consiste en des jeux de fonctions
complétées par l'électron électronique cusp- ![]() l'équation 4.10 et l'homogène
l'équation 4.10 et l'homogène
![]()
![]() - le terme dépende, de l'équation 4.11. On le montre schématiquement dans
la figure(le chiffre) 4. 1. { 4.1}
- le terme dépende, de l'équation 4.11. On le montre schématiquement dans
la figure(le chiffre) 4. 1. { 4.1}
![\includegraphics [width=10cm] {Figures/acjast.eps}](pkthimg339.gif) |
Pour les applications principales dans cette thèse, seulement les termes ![]() ont
été utilisés et des résultat satisfesant ont été obtenue et la pleine série a dû encore
être mise en oeuvre. Dans les derniers essais l'état
d'un atome d'oxygène tout-électronique, utilisant l'exact orbite,
ont
été utilisés et des résultat satisfesant ont été obtenue et la pleine série a dû encore
être mise en oeuvre. Dans les derniers essais l'état
d'un atome d'oxygène tout-électronique, utilisant l'exact orbite,
![]() de l'énergie de corrélation expérimentale a été obtenu utilisant tous les termes, approximatif
de l'énergie de corrélation expérimentale a été obtenu utilisant tous les termes, approximatif
![]() plus qu'une wavefunction l'utilisation seul
plus qu'une wavefunction l'utilisation seul ![]() des différents termes. Cette
exactitude est semblable à s'elle obtenue dans
les calculs pseudopotentiels d'atomes d'oxygène, démontrant l'importance
des termes de corrélation complémentaires en traitant des électrons fondamentaux.
des différents termes. Cette
exactitude est semblable à s'elle obtenue dans
les calculs pseudopotentiels d'atomes d'oxygène, démontrant l'importance
des termes de corrélation complémentaires en traitant des électrons fondamentaux.